2015年算法设计题
1、层序遍历二叉树
考一个基本的层序遍历，那这里为了方便展示效果，我直接创了一个BST，大家也可以把代码复制一下运行一下结果
typedef struct node
{
int data;
int layer;
struct node *lchild,*rchild;
}TREE,*listtree;
//那我这里初始化是直接给了一个节点了，并且赋值了，大家如果给个空也是可以的
bool Inittree(listtree &T)
{
T=(TREE*)malloc(sizeof(TREE));
if(T!=NULL)
{
T->data=14;
T->layer=1;
T->lchild=NULL;
T->rchild=NULL;
}
return true;
}
void insert_node_bst(listtree &T,int e)
{
if(T==NULL)
{
T=(TREE*)malloc(sizeof(TREE));
T->data=e;
T->lchild=NULL;
T->rchild=NULL;
}
if(e == T->data)
return ;
else if(e < T->data)
insert_node_bst(T->lchild,e);
else
insert_node_bst(T->rchild,e);
}
void visit(listtree T)
{
if(T!=NULL)
cout<<T->data<<" ";
}
//这个函数是为了判断该树是否为二叉排序树，这个题是不需要的，是附带的
//当然这也是2018年算法设计的最后一题，这里大家看一眼就好，到后面我会具体说这个
void inorder_pro(listtree &T)
{
if(T!=NULL)
{
inorder_pro(T->lchild);
if(T->lchild!=NULL && T->lchild->data > T->data)
{
cout<<"the tree isn't a bst_treee!!!!"<<endl;
tag=1;
exit(0);
}
if(T->rchild!=NULL && T->rchild->data < T->data)
{
cout<<"the tree isn't a bst_treee!!!!"<<endl;
tag=1;
exit(0);
}
inorder_pro(T->rchild);
}
}
//****************【正常的层序遍历】*******************
void level_order(listtree &T)
{
queue<TREE*> q;
TREE *p=T;
q.push(T);
while(!q.empty())
{
p=q.front();
q.pop();
visit(p);
if(p->lchild!=NULL)
q.push(p->lchild);
if(p->rchild!=NULL)
q.push(p->rchild);
}
}
int main()
{
//创建一棵树
listtree T;
Inittree(T); //初始化
//我这里直接很暴力的添加节点了，就不在命令行输入了，因为那样不好调试
insert_node_bst(T,3);
insert_node_bst(T,1);
insert_node_bst(T,6);
insert_node_bst(T,8);
insert_node_bst(T,28);
insert_node_bst(T,17);
insert_node_bst(T,16);
inorder(T);
cout<<endl<<"----------------------------------"<<endl;
//判断二叉树是否是二叉排序树
inorder_pro(T);
if(tag==0)
cout<<"this tree is a bst_tree!!!!!";
cout<<endl<<"----------------------------------"<<endl;
//这里就是层序遍历的函数入口啦
level_order(T);
return 0;
}2、设计一个带头节点的循环链表来表示队列，并且设一个尾指针，然后编写相应的队列初始化、入队，出队操作的算法，那思路如下：
- 首先循环链表框架写出来，然后我们用一个全局指针作为尾指针
- 初始化就是创建一个头节点
- 入队操作就是链表的后插操作，出队就是删除第一个节点，区别就是入队和出队都需要用到尾指针，也就是用尾指针来确定你要插入或者删除的节点
#include<iostream>
using namespace std;
typedef struct Node
{
int data;
struct Node *next;
}Lnode,*List;
//我们把尾指针和链表L设置为全局，这样方便实现该算法，你要写局部也可以的
Lnode *tail;
List L;
bool Initlist(List &L)
{
L=(Lnode*)malloc(sizeof(Lnode));
if(L==NULL)
return false;
L->next=L;
L->data=0;
tail=L; //把尾指针指向头节点，后面我们就用tail来定位了
return true;
}
//用尾指针来做入队处理，也就是链表的后插法
bool enqueue(int e)
{
if(tail==NULL)
return false;
Lnode *s=(Lnode *)malloc(sizeof(Lnode));
s->data=e;
s->next=tail->next;
tail->next=s;
tail=s; //这一步很重要，你不要插入完节点就不管了，你得把尾指针也处理了，也就是指向当前的尾节点
return true;
}
//出队步骤，也就是把第一个节点删除
int dequeue()
{
Lnode *q;
int temp;
q=tail->next->next;
temp=q->data;
tail->next->next=q->next;
free(q);
return temp;
}
int main()
{
Initlist(L); //初始化链表
enqueue(10);
enqueue(20);
enqueue(30);
enqueue(40);
enqueue(50);
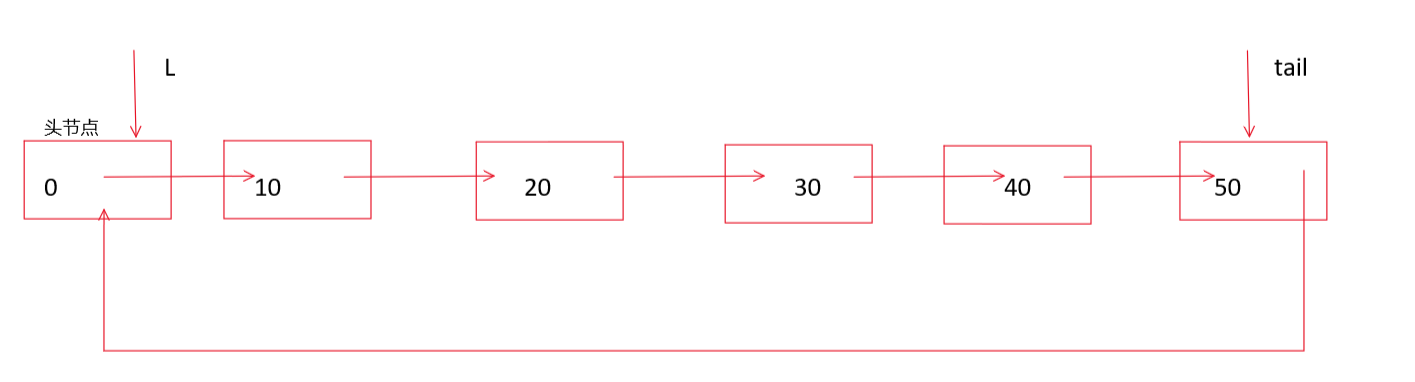
//到这里可以看下下面的图，循环链表的样子
//遍历一下这个队列（链表）的元素
Traverse_List(L);
for(int i=0;i<3;++i)
{
cout<<"The value of the node to be deleted is:"<<dequeue()<<endl;
}
//看下出对了3个元素，还剩下那些节点
Traverse_List(L);
return 0;
}
2016年算法设计题
将两个增序链表合成一个增序的链表，且不开辟新的节点，设计思路如下：
先说一下这个题似乎规定了不能使用附加节点，那可爱的理解是不创建第三个链表用来存储最终的序列，我们只在原有链表进行操作，不新添加任何节点，也就是不用new，malloc，我翻了下参考书关于这个题的答案，是用第三个链表存储的。
-
我们将L1作为最后的结果链表
-
同时用两个指针遍历两个L1,L2链表，当L2中的值大于L1中的值，将L2当前节点插入L1
-
合并逻辑（merge函数）：
- 1、如果p1和p2有一个指针已经指向了其所在链表的尾节点，那么把L2的节点打包给到L1即可。
- 2、如果p1，p2均没有指向最后一个节点，那么就把p2指向的当前节点插入到链表L1即可
-
我们定义了三个函数：find，insertnextnode，listinsert
- find：是一个辅助函数，在表L1中找到那个要插入的位置，如果在代码中把find的部份去掉就会出错，原因如下图
- insertnextnode：已经定位好后插的位置，使用该函数叫新建立的节点插入到该位置
- listinsert：这是一个按位序插入节点的函数，配合
insertnextnode使用，在该算法中用来创建节点
那执行代码如下,有一丢丢长：
#include<iostream>
using namespace std;
typedef struct node
{
int data;
struct node *next;
}Lnode,*List;
List L1;
List L2;
bool Initlist(List &L)
{
L=(Lnode*)malloc(sizeof(Lnode));
if(L==NULL)
return false;
L->data=0;
L->next=NULL;
return true;
}
//这个是插入到指定结点的后面
bool InsertNextNode(Lnode *p,int e)
{
if(p==NULL)
return false;
Lnode *s=(Lnode *)malloc(sizeof(Lnode));
s->data=e;
s->next=p->next;
p->next=s;
return true;
}
//按位序插入，是从1开始的，不是从0
bool ListInsert(List &L,int i,int e)
{
if(i<1)
return false;
Lnode *p=NULL;
int j=0;
p=L;
while(p!=NULL && j<i-1)
{
p=p->next;
j++;
}
return InsertNextNode(p,e);
}
bool Traverse_List(List &L)
{
//用一个指针遍历一下，别直接用L去遍历，否则链表就没了
Lnode *p = L->next;
while (1)
{
if (p->next!=NULL)
cout << p->data << "->";
else if(p->next == NULL)
{
cout << p->data;
break;
}
p = p->next;
}
cout << endl;
return true;
}
Lnode *find(Lnode *p,int e)
{
while(1)
{
if(p->next!=NULL && p->next->data<e) //这里注意啊，如果p是L1的最后一个节点，那么就不用找了，直接把这个p的地址返回就好了，因为后面没有节点了
{
p=p->next;
}
else
break;
}
return p;
}
//我们把L1作为最后的合成链表，也就是把L2的元素插入到L1
bool merge(List list1,List list2)
{
Lnode *p1,*p2; //p1是L1链表的操作指针，p2是L2链表的操作指针
p1=list1->next;
p2=list2->next;
while(1)
{
if(p1->next==NULL||p2->next==NULL)
{
p1->next=p2;
list2->next=NULL;
break;
}
else if(p1->next!=NULL||p2->next!=NULL)
{
if(p1->data<=p2->data) //保证稳定性（就排序算法的稳定性），嘿嘿
{
//说明需要把p2插入到p1
p1=find(p1,p2->data);
//找了要插入的位置
Lnode *temp;
temp=p2->next;
p2->next=p1->next;
p1->next=p2;
list2->next=temp;
p2=temp;
p1=p1->next;
}
else
p1=p1->next;
}
}
return true;
}
int main()
{
Initlist(L1);
ListInsert(L1,1,10);
ListInsert(L1,2,30);
ListInsert(L1,3,50);
Initlist(L2);
ListInsert(L2,1,11);
ListInsert(L2,2,40);
ListInsert(L2,3,60);
ListInsert(L2,4,70);
ListInsert(L2,5,100);
Traverse_List(L1);
cout<<"------------------------------"<<endl;
Traverse_List(L2);
cout<<"------------------------------"<<endl;
if(L1->next->data<L2->next->data)
{
merge(L1,L2);
Traverse_List(L1);
}
else
{
merge(L2,L1);
Traverse_List(L2);
}
return 0;
}2017年算法设计题
1、二叉树用二叉链表作为存储结构，求前序序列中处于第K个位置的节点，思路如下：
- 为了方便，我们用BST来实现这个算法
- 求前序序列第K个位置，我们用一个全局count来记录当前遍历节点的个数，然后再visit函数中进行判断当
count==K时即可求出该结点，然后输出即可。
#include<iostream>
using namespace std;
typedef struct node
{
int data;
struct node *lchild,*rchild;
}Tnode,*Tree;
int _count=0;
bool Inittree(Tree &T)
{
T=(Tnode*)malloc(sizeof(Tnode));
if(T!=NULL)
{
T->data=14;
T->lchild=NULL;
T->rchild=NULL;
}
return true;
}
void insert_node_bst(Tree &T,int e)
{
if(T==NULL)
{
T=(Tnode*)malloc(sizeof(Tnode));
T->data=e;
T->lchild=NULL;
T->rchild=NULL;
}
if(e == T->data)
return ;
else if(e < T->data)
insert_node_bst(T->lchild,e);
else
insert_node_bst(T->rchild,e);
}
void visit(Tree &T,int num)
{
_count++;
if(T!=NULL && _count==num)
{
cout<<T->data<<endl;
}
}
void preorder(Tree &T,int num)
{
visit(T,num);
preorder(T->lchild,num);
preorder(T->rchild,num);
}
int main()
{
Tree T;
Inittree(T);
insert_node_bst(T,2);
insert_node_bst(T,5);
insert_node_bst(T,7);
insert_node_bst(T,1);
insert_node_bst(T,27);
preorder(T,3);
return 0;
}2、简单创建一个链表，然后判断一下即可，用一个flag标志位来记录是否为等差数列，当然也可以不用，直接再func函数输出结果也行的。
#include<iostream>
using namespace std;
typedef struct node
{
int data;
struct node *next;
}Lnode,*List;
bool Init(List &L)
{
L=(Lnode*)malloc(sizeof(Lnode));
if(L==NULL)
return false;
L->next=NULL;
L->data=0;
return true;
}
//这个是插入到指定结点的后面
bool InsertNextNode(Lnode *p,int e)
{
if(p==NULL)
return false;
Lnode *s=(Lnode *)malloc(sizeof(Lnode));
s->data=e;
s->next=p->next;
p->next=s;
return true;
}
//按位序插入，是从1开始的，不是从0
bool ListInsert(List &L,int i,int e)
{
if(i<1)
return false;
Lnode *p=NULL;
int j=0;
p=L;
while(p!=NULL && j<i-1)
{
p=p->next;
j++;
}
return InsertNextNode(p,e);
}
int temp=0,flag=0;
int func(List &L)
{
Lnode *p1,*p2;
p1=L->next;
p2=L->next->next;
temp=(p2->data)-(p1->data);
while(p1->next)
{
if( temp==(p2->data)-(p1->data))
{
flag=1;
p1=p1->next;
p2=p2->next;
}
else
flag=0;
}
return flag;
}
bool Traverse_List(List &L)
{
//用一个指针遍历一下，别直接用L去遍历，否则链表就没了
Lnode *p = L->next;
while (1)
{
if (p->next!=NULL)
cout << p->data << "->";
else if(p->next == NULL)
{
cout << p->data;
break;
}
p = p->next;
}
cout << endl;
return true;
}
int main()
{
List L;
Init(L);
ListInsert(L,1,20);
ListInsert(L,2,30);
ListInsert(L,3,40);
ListInsert(L,4,50);
Traverse_List(L);
int temp=func(L);
if(temp==1)
cout<<"yes!!!"<<endl;
else
cout<<"NO!!!"<<endl;
return 0;
}2018年算法设计题
1、
2、判断二叉树是否为二叉排序树，具体思路如下：
- 先创建一个树，那我们这里是直接创建了一个BST
- 然后借用中序遍历来判断该树是否为BST，因为中序遍历在BST中是一个增序序列，所以只需要在visit函数中判断该点的左右孩子是否满足要求即可，这里我们用一个标志位tag，tag初始化为0，如果在中序遍历中发现不满足BST的要求，就把
tag==1。最后通过tag的值来判断是否为BST。
#include<iostream>
#include<queue>
#include<stack>
using namespace std;
typedef struct node
{
int data;
int layer;
struct node *lchild,*rchild;
}TREE,*listtree;
bool Inittree(listtree &T)
{
T=(TREE*)malloc(sizeof(TREE));
if(T!=NULL)
{
T->data=14;
T->layer=1;
T->lchild=NULL;
T->rchild=NULL;
}
return true;
}
void insert_node_bst(listtree &T,int e)
{
if(T==NULL)
{
T=(TREE*)malloc(sizeof(TREE));
T->data=e;
T->lchild=NULL;
T->rchild=NULL;
}
if(e == T->data)
return ;
else if(e < T->data)
insert_node_bst(T->lchild,e);
else
insert_node_bst(T->rchild,e);
}
//判断BST的核心代码
int tag=0;
void inorder_pro(listtree &T)
{
if(T!=NULL)
{
inorder_pro(T->lchild);
if(T->lchild!=NULL && T->lchild->data > T->data)
{
cout<<"the tree isn't a bst_treee!!!!"<<endl;
tag=1;
exit(0);
}
if(T->rchild!=NULL && T->rchild->data < T->data)
{
cout<<"the tree isn't a bst_treee!!!!"<<endl;
tag=1;
exit(0);
}
inorder_pro(T->rchild);
}
}
int main()
{
listtree T;
Inittree(T);
insert_node_bst(T,3);
insert_node_bst(T,1);
insert_node_bst(T,6);
insert_node_bst(T,8);
insert_node_bst(T,28);
insert_node_bst(T,17);
insert_node_bst(T,16);
inorder(T);
cout<<endl<<"----------------------------------"<<endl;
//判断二叉树是否是二叉排序树
inorder_pro(T);
if(tag==0)
cout<<"this tree is a bst_tree!!!!!";
}2021年算法设计题
1、编写一个C语言程序，从命令行传入一个文件名和要保存到该文件的字符串，在程序中保存到文件。
那这个代码有很多种写法，我写两个C++版本供大家参考，C的话白皮书答案就有这里就不写了：
版本一：C++用流对象写入
#include<iostream>
#include<fstream>
using namespace std;
int main(int argc, char *argv[])
{
if(argc!=3)
{
cout<<"Wrong number of parameters"<<endl;
exit(0);
}
fstream outfile;
outfile.open(argv[1],ios::out);
if(!outfile)
{
cout<<argv[1]<<"failed to open"<<endl;
exit(0);
}
outfile<<argv[2]<<endl;
outfile.close();
return 0;
}然后运行即可，如下图：
版本二：C++二进制读写
#include<iostream>
#include<fstream>
#include<cstring>
using namespace std;
int main(int argc,char *argv[])
{
if(argc!=3)
{
cout<<"Wrong number of parameters"<<endl;
exit(0);
}
ofstream os(argv[1],ios_base::out|ios_base::binary);
int temp=strlen(argv[2]);
os.write(argv[2],temp);
os.close();
//正常代码到这里就结束了，只是因为我们是二进制写入，大家进入1.txt文本中看是乱码，所以我额外写了一个
//二进制读把文本中我们写入的内容显示出来，这样证明我们写入是没问题的
ifstream is(argv[1],ios_base::in|ios_base::binary);
if(is)
{
is.read(argv[2],temp);
//cout<<dt2.day<<" "<<dt2.mon<<" "<<dt2.year<<endl;
cout<<argv[2];
}
else
{
cout<<"ERROR:cannot open file"<<endl;
}
is.close();
return 0;
}代码结果：
2、用C语言编写一个递归函数，计算一个数的阶层。同2022年，大家可以跳到2022年看这个题的解答
3、写一个模板类：
#include<iostream>
#include<fstream>
using namespace std;
template<class T>
class A
{
private:
T x,y;
public:
A(T a, T b):x(a),y(b){}
void add()
{
cout<<x+y<<endl;
}
};
int main()
{
A<int> a(10,20);
A<float> b(11.1,22.2);
A<char> c('a','b');
a.add();
b.add();
c.add(); //ascill码值相加啊，不是子串拼接
return 0;
}运行结果：
4、有n个不可分割的物品，现有一个背包，容量为B。应该如何向背包装入物品，使其背包价值之和最大，很明显了对吧，就是经典且朴素的0-1背包问题，那这个题在动态规划章节中详细讲解了，大家可以点击动态规划（一）来看完整版，那这里就放一个二维数组版本的代码，嘻嘻~~~
#include<iostream>
#include<vector>
using namespace std;
vector<int> weight={1,3,4};
vector<int> value={15,20,40};
int bag_weight=4;
//这一步就是给“二维数组”赋值为全0
vector<vector<int>> dp(weight.size(),vector<int>(bag_weight+1,0));
void beibao()
{
//初始化，不要全给0，那是憨憨,解释一下j-weight[0]就是当前包的容量——这个0号物体的重量还剩多少，也可能不够装
for(int i=bag_weight;i>=weight[0];i--)
{
dp[0][i]=dp[0][i-weight[0]]+value[0];
}
//更新dp数组，这里就是dp的精髓了,从dp[1][1]开始更新啊，别傻乎乎的dp[0][0]开始
for(int i=1;i<weight.size();i++)
{
for(int j=1;j<=bag_weight;j++)
{
if(j < weight[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]); //精髓所在
}
}
//最后输出二维数组右下角的数，这个数就是背包可以装的最大容量
cout<<dp[weight.size()-1][bag_weight];
}
int main()
{
beibao();
return 0;
}2022年算法设计题
1、这个题可爱没有看懂它让我干嘛，那这里就先不写啦！！！后期如果想到了会更新滴！！！
2、用C语言编写一个递归函数，计算一个数的阶乘。这个题比较简单，但有一个点想特别强调一下，先看下正确代码：
#include<iostream>
using namespace std;
int func(int num)
{
if(num==1||num==0) //递归出口
return 1;
return num*func(num-1); //递归入口，这一步我会在下面特别说明
}
int main()
{
int a;
cin>>a;
cout<<func(a);
return 0;
}上面的代码有一个地方我想特别说明一下，如下图：
3、比较经典又朴素的最大子序列和，题目说如果序列值全为负数，则输出0，且尽可能高效。
关于最大子序列和，我在动态规划（二)中给大家做了完整的解释，还给大家拓展了一些关于子序列的题，如果忘记了的或者还没有看过的小伙伴可以先去瞅一眼。那这里我就用动态规划来实现这个算法，时间复杂度O（n）。
这题需要稍微改动一下，题目说如果序列值全为负数，需要输出0，而我们的动态规划，贪心等解题的方式是没有这个的，所以这个题需要用一个标志位flag来进行一个处理，具体如下
#include<iostream>
#include<vector>
using namespace std;
vector<int> arr={-2,-1,-10,-20,-21,-5,-9};
vector<int> dp(arr.size());
int result;
int flag=0; //0表示当前数为负数，1为正整数
void func()
{
dp[0]=arr[0];
if(dp[0]>=0) //这里对第一个数组元素进行特判
flag=1;
result=dp[0];
for(int i=1;i<dp.size();i++)
{
dp[i]=max(dp[i-1]+arr[i],arr[i]);
if(dp[i]>result)
result=dp[i];
if(dp[i]>=0)
flag=1;
}
//如果代码执行到这里，flag依旧为0，说明整个数组都是负数，输出0，否则输出result
//这里要注意，不是result是负数就说明整个数组都是负数，例如{-2，1}，这个序列的result=-1
//但并没有全部都是负数
if(flag==0)
cout<<"0"<<endl;
else
cout<<result<<endl;
}
int main()
{
func();
return 0;
}
Comments | 2 comments
Your blog consistently captivates me throughout. I cannot stop reading without absorbing every word you write.
Your blog engages me from the beginning to the end. I can never move on without devouring your entire post.