
0-1背包问题(动态规划的做法,不是回溯)
0-1背包问题有很多解法,这里我们用动态规划做,暴力破解我后续会写出来,因为涉及到回溯,所以我会在回溯中介绍这个。
0-1背包是干啥的大家肯定都不陌生了,最简单最朴素的就是当前有n个物品每个物品有自己价值且物品不可拆分,有一个容量m的背包,问这个背包如何装物品可以使得价值最大。
那我们就用一个具体的例子来解释这个问题:
首先我们有一个物品清单和一个容量为4背包,如下图:
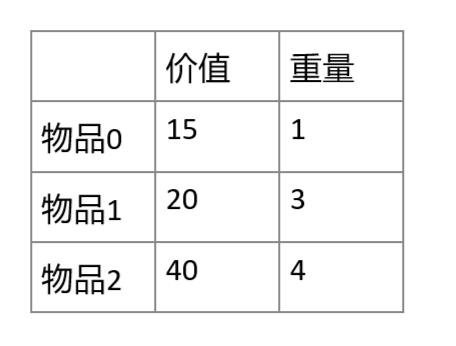
直观上,大家肯定可以得出答案,就是单方物品2是价值最大的。但代码如何实现呢?
这里先做一些准备工作,我们需要dp二维数组(下图绿色框框),以及一个weight数组,value数组分别存放物品的重量和价值,还有一个bag_weight存放包的容量,那这里为了直观解释,我们做了一些改动,具体如下图:

数组准备好后,我们开始往里面填充数值,这个表格就是这个算法的核心,我概括了一下,大致分为3步,也就是三步走:
- 第一步:初始化,也就是把第0行和第0列分别进行初始化,代码如下:
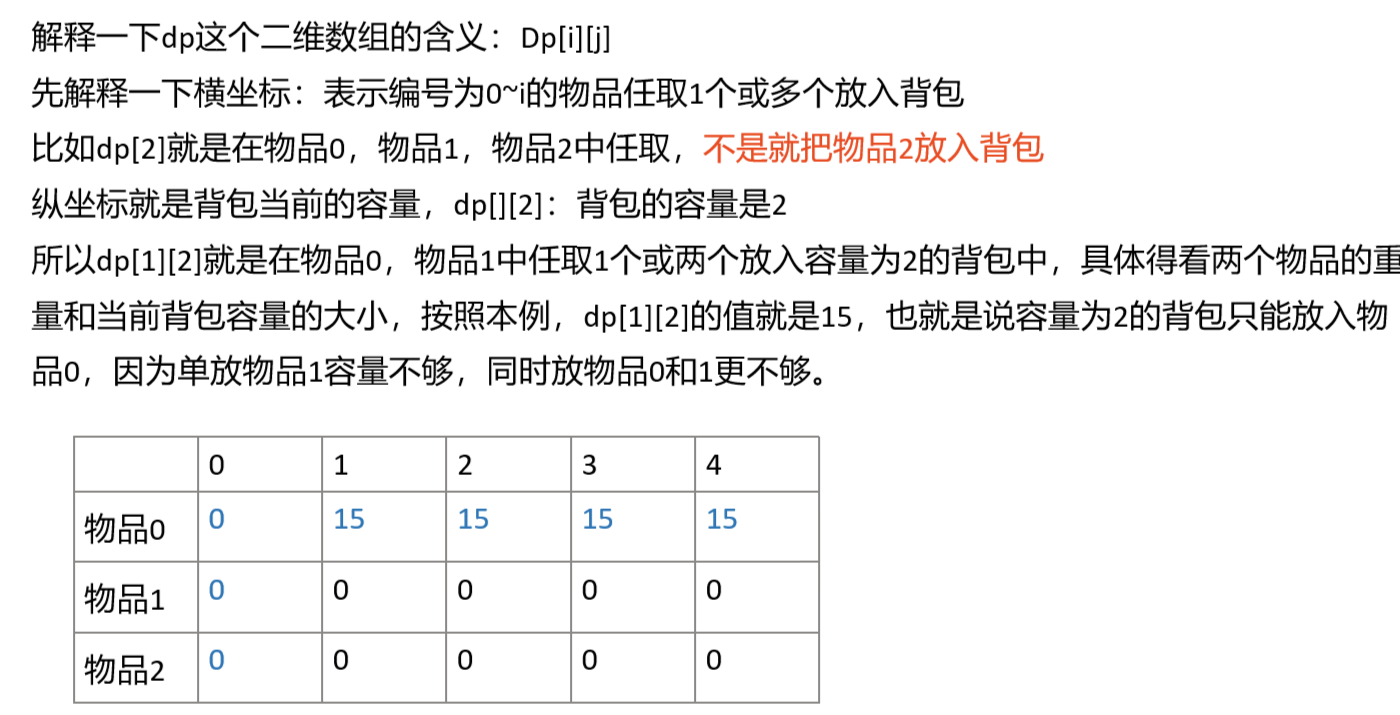
for(int i=bag_weight;i>=weight[0];i--)
{
dp[0][i]=dp[0][i-weight[0]]+value[0];
}对上面的代码我做如下解释,见下图:
至此初始化工作完成,这里提一嘴,可不可以不初始化,直接把整个数组赋值为0,这不好嘛?
答:不可以,这个例子是没问题,但其他题大概率是不行的,原因可以自己想一下。
这里再解释一下表格中数据的含义,方便后面大家对代码的理解。

- 第二步:遍历(更新)二维数组剩余部份,代码如下:
for(int i=1;i<weight.size();i++)
{
for(int j=1;j<=bag_weight;j++)
{
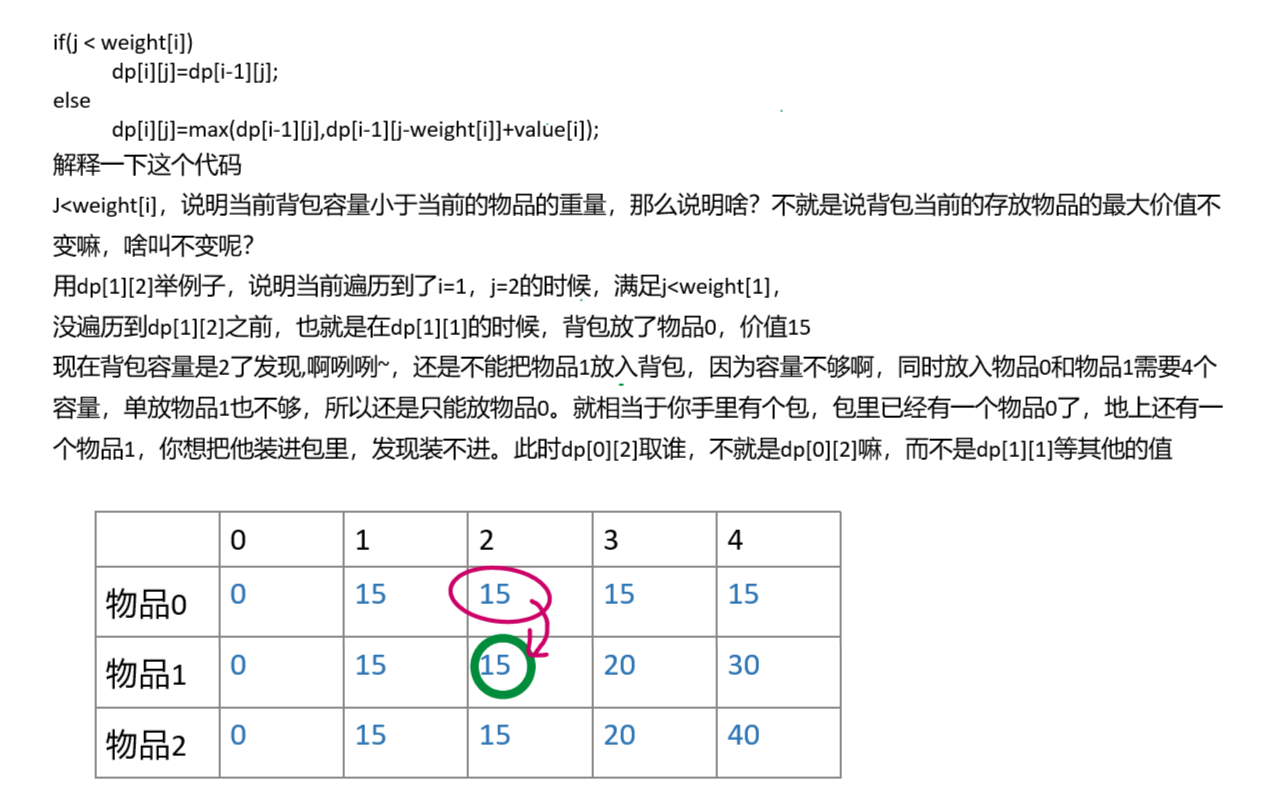
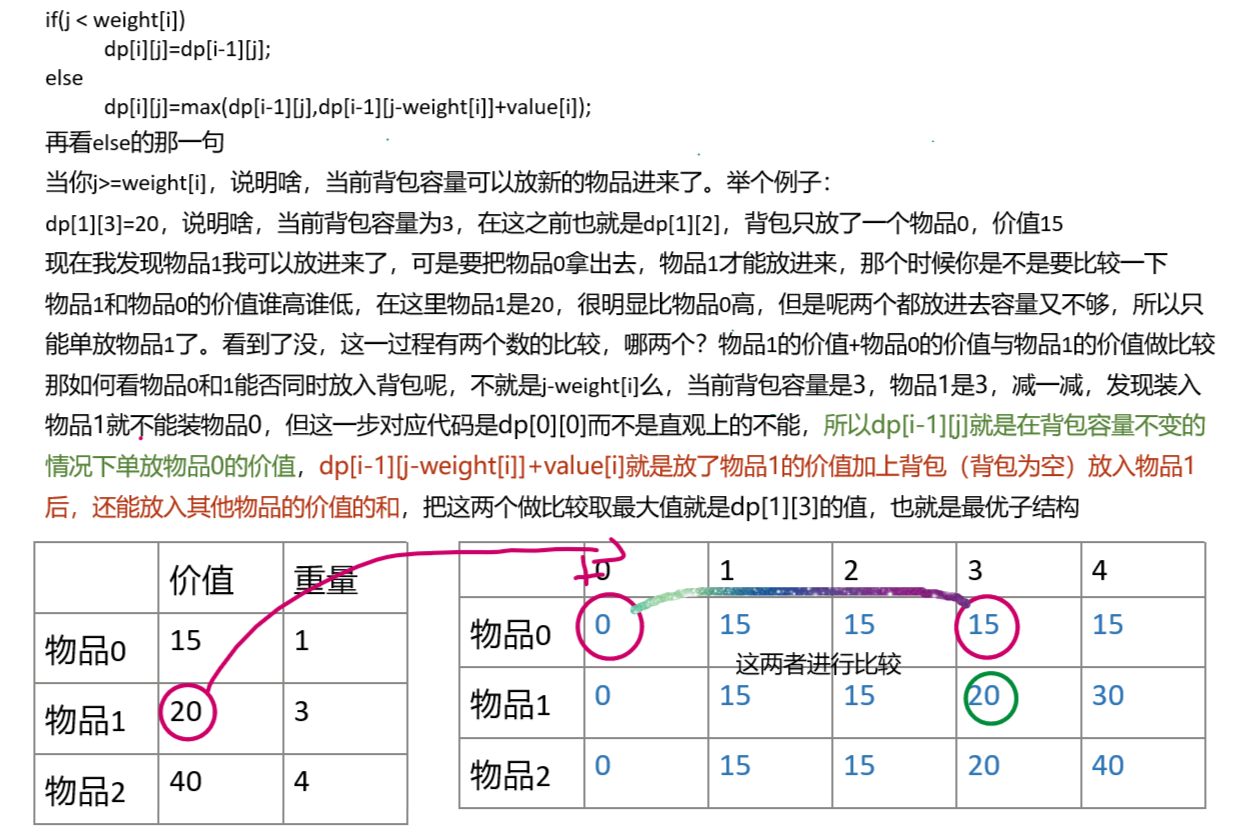
if(j < weight[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]); //精髓所在
}
}上述代码使用双循环来遍历更新数组内容,其中外循环是遍历物品,内循环是遍历背包的容量,具体解释见下图:
- 第三步:输出最后的结果,也就是最右下角的数
下面是完整代码,大家可以运行一下,感受一下代码具体的细节:
#include<iostream>
#include<vector>
using namespace std;
vector<int> weight={1,3,4};
vector<int> value={15,20,40};
int bag_weight=4;
//这一步就是给“二维数组”赋值为全0
vector<vector<int>> dp(weight.size(),vector<int>(bag_weight+1,0));
void beibao()
{
//初始化,不要全给0,那是憨憨,解释一下j-weight[0]就是当前包的容量——这个0号物体的重量还剩多少,也可能不够装
for(int i=bag_weight;i>=weight[0];i--)
{
dp[0][i]=dp[0][i-weight[0]]+value[0];
}
//更新dp数组,这里就是dp的精髓了,从dp[1][1]开始更新啊,别傻乎乎的dp[0][0]开始
for(int i=1;i<weight.size();i++)
{
for(int j=1;j<=bag_weight;j++)
{
if(j < weight[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]); //精髓所在
}
}
//最后输出二维数组右下角的数,这个数就是背包可以装的最大容量
cout<<dp[weight.size()-1][bag_weight];
}
int main()
{
beibao();
return 0;
}0-1背包问题——一维数组(滚动数组)
上面我们介绍了0-1背包的动态规划的解法,用一个dp二维数组来存放背包的状态,但其实大家如果掌握的熟练其实很快就可以发现其实dp二维数组中是有状态的重叠的,啥意思呢?见下图:
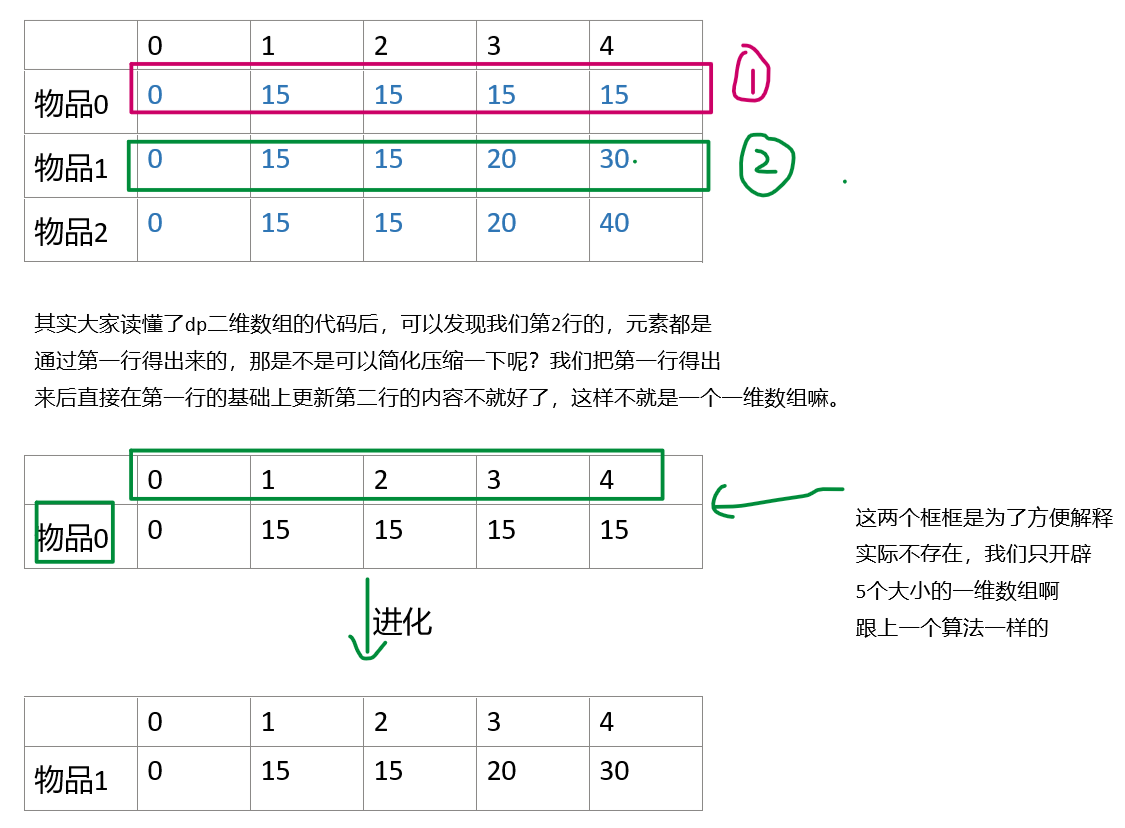
上图解释了为啥可以用一维数组存储这个结果,说白话就是一维数组可以重复利用,直接把二维数组中的上一层拷贝到下一层。
那下面我们来实际操作一下,还是那之前的例子,同样的一个weight数组,一个value数组,一个bag_weight变量:

接下来就是dp的五步走:
- 1、确定dp数组的含义
之前我们用二维数组的时候,dp[i][j]的含义还记得嘛?不记得赶紧往上翻去复习。这里用一维数组,那么就是dp[j]。仔细看,我写的是dp[j],而不是dp[i]哦。这么写就是为了匹配二维数组,这里写dp[j]就是背包容量为j时最大价值,也就是说j依旧表示背包容量。
- 2、dp数组的递推公式,大家自行理解,和二维数组的递归公式差不多的。
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);- 3、dp一维数组的初始化
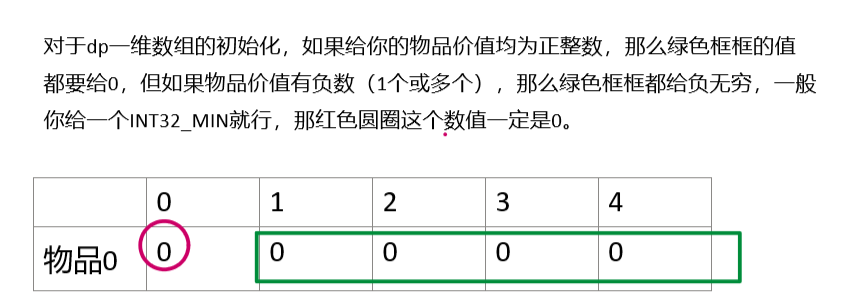
- 4、确定遍历(更新)dp数组的顺序,谁在前谁在后,循环从前往后还是从后往前
for(int i=0;i<weight.size();i++)
{
for(int j=bag_weight;j>=weight[i];--j)
{
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
}
}我解释一下上述代码的一些细节问题:

- 5、遍历(更新)数组,不熟练就在纸上把数组得元素填满感受一下
下面给出完整代码,供大家体会理解,也可以单步调试:
#include<iostream>
#include<vector>
using namespace std;
vector<int> weight={1,3,4};
vector<int> value={15,20,40};
int bag_weight=4;
vector<int> dp(bag_weight,0);
void func()
{
for(int i=0;i<weight.size();i++)
{
for(int j=bag_weight;j>=weight[i];--j)
{
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
}
}
cout<<dp[bag_weight]<<endl;
}
int main()
{
func();
return 0;
}



Comments | NOTHING