矩阵连乘
这节内容我们来讲一下矩阵连乘问题,先看下啥是矩阵连乘:

那上图就是矩阵连乘的大致解释,但我接下来要解释一下细节的东西,防止小伙伴们往下看的时候会一头雾水:

那为啥矩阵连乘可以用动态规划呢?大家可以自行判断:①.最优子结构 ②.子问题重叠。
OK,那既然用动态规划来做,那么依旧是五步走:
1、确定dp数组的含义
大家先想一下这个题的dp是一个二维数组还是一维数组,还是两个都可以?
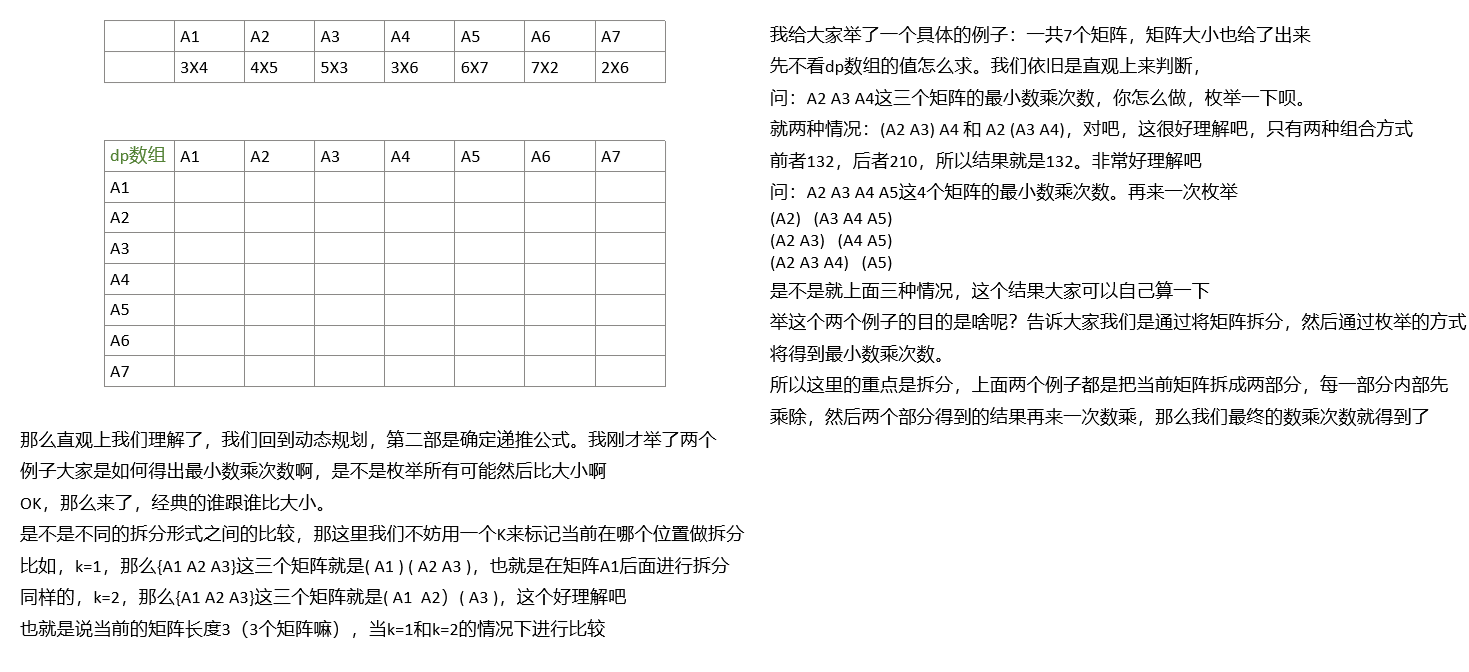
答案是都可以(很多人可能学过这个矩阵连乘,认为是二维,其实一维也可以,后面我会解释)。我们先用二维来实现,确定一下dp[i][j]的含义。也就是矩阵1~i的最小数乘次数,具体见下图:

2、确定递推公式,这个稍后做解释
3、dp数组的初始化,这个稍后做解释
4、确定遍历dp数组的顺序
我们已经默认采用二维数组,那两重循环跑不掉了,但两重循环够了吗?答案是不够,稍后做解释
5、遍历(更新)dp数组
那接下来我们进入重点,如何求这个dp[i][j]。
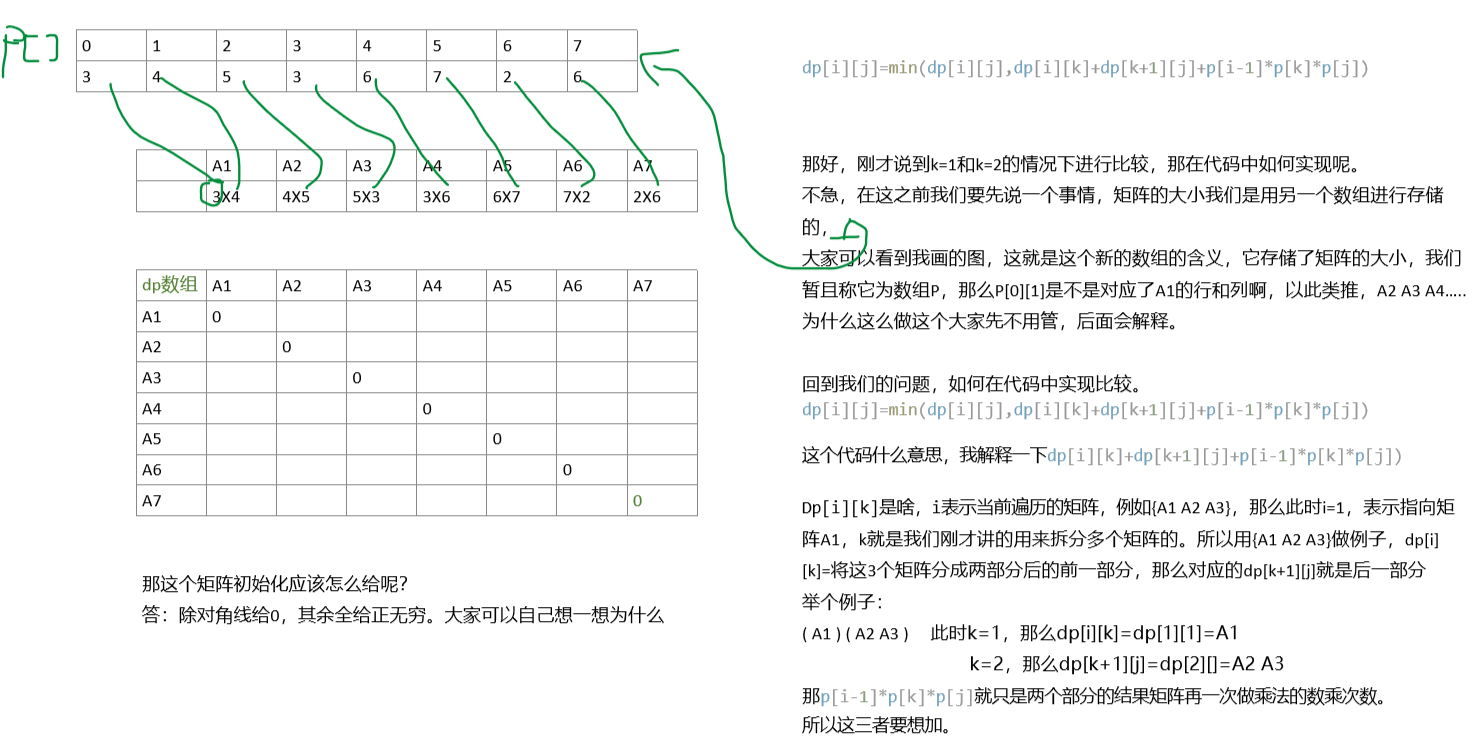
接下来给大家一个矩阵乘法的代码,大家可以看一看,自己画图试一试:(不是执行代码哦!!!!)
vector<int> p={3,4,5,3,6,7,2,6};
int n=p.size()-1;
vector<vector<int>> dp(p.size(),vector<int>(p.size(),INT32_MAX));
void func()
{
for(int d=2;d<=n;d++)
{
for(int i=1;i<=n-d+1;i++)
{
int j=i+d-1;
dp[i][j]=INT32_MAX;
for(int k=i;k<j;k++)
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j]);
}
}
cout<<dp[1][p.size()-1]<<endl;
}那我把上面的例子的dp数组的结果给大家打印一下,大家可以感受一下,看看是否能发现点什么:
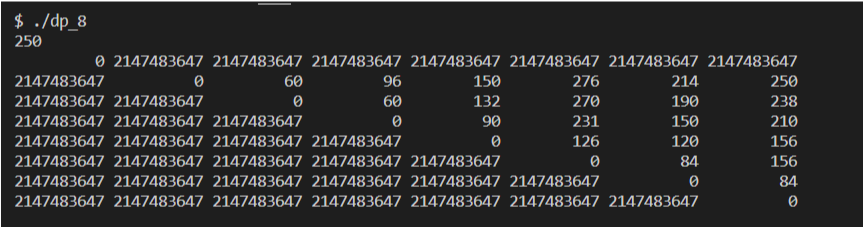
可能会有小伙伴觉得,哎?你这跟书上的代码不一样耶,为啥呀?
真的不一样吗?其实是一样的,书上多了一个数组用来记录k拆分的位置,这样可以输出数乘次数最少的拆分结果,除此之外都是一样的,大家可以仔细品一品,也是把min那一步拆成两步写了,为了方便用数组记录k拆分的位置。
可能又会有小伙伴问,哎?为啥不给执行代码啊,那我咋运行看结果啊,我也没法单步调试啊。
是这样的,矩阵乘法本身不是一个具体的题,不同于子序列和,它是一个解决某些具体问题的方法,而这个方法用动态规划实现。
那为了更加形象,我给大家准备了一个题:
乘法游戏是用一些牌来玩的,在每张牌上都有-一个正整数。玩家从一行牌中取出一-张牌, 得分的数量等于所取牌上的数字与左右两张牌上的数字的乘积。不允许取出第一张和最后一张牌。 经过最后一步后,只剩下两张牌。玩牌的目标是把得分的总数降到最低。例如,若一行牌包含数字10、1、50、20、5,则若玩家先拿出一张1,然后拿出20和50的牌,得分便是10x lx50+50x20x5+10x50x5=500+5000+2500-8000.若他按相反的顺序拿牌,即50、20、1,则得分是1x50x20+1x20x5+10x 1x5=1000+ 100+50=1150。
那这个题就是用矩阵乘法来做,大家可以感受一下,这个题所给的数字就是上面所讲的p数组。
石子合并
石子合并其实和矩阵连乘的逻辑差不多的,区别就在状态转移方程上,整体的实现方式是和矩阵连乘很相似的,大家看完就会发现,无论是dp二维数组还是最终的输出都是和矩阵连乘类似的。
那我们先上一个具体的题让大家感受一下什么样的问题会用到石子合并。
设有N堆石子拍成一排,其编号为1、2、3...N。
每堆石子有一定的质量,可以用一个整数来描述,现在要将这N堆石子合并成为一堆。 每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并时由于选择的顺序不同,合并的总代价也不相同。
问题是:找出一种合理的方法,使总的代价最小,输出最小代价。
例如:一共5堆石子,每堆石子的重量分别为1、3、4、2、5。合并的代价最小是34。
看完以上的问题,大家直观上怎么解决?可以先画个图,然后每次只合并在当前状态下代价最小的,然后得出最小代价。如下图:
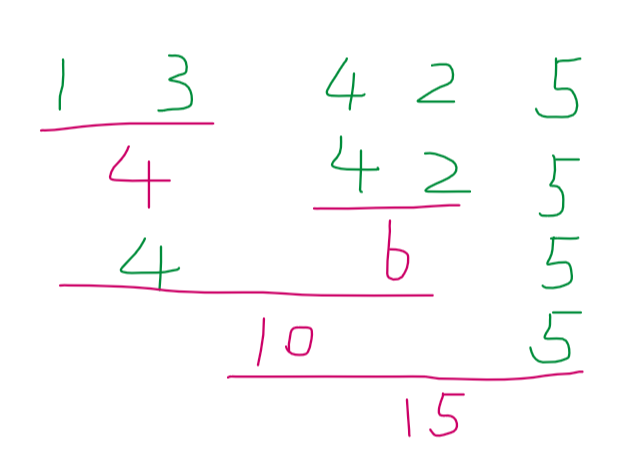
上图就是比较容易想到的计算代价的方式,那这种方法就是贪心。对吧?每次都取当前状态的最优解,也就是局部最优解,但这能得到全局最优解嘛?也就是说4+6+10+15=35是不是最小的代价了呢?我们看下面一种合并顺序:
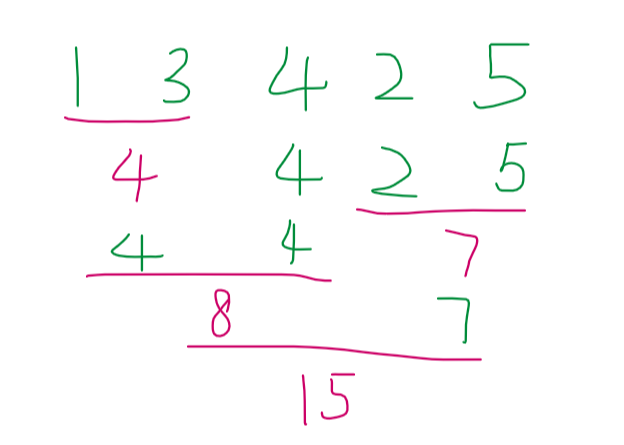
大家自己算一下这个合并的代价是多少?是不是4+7+8+15=34。哎?居然比贪心还少耶?对哒,在这个题,贪心的局部最优解最终得不到全局最优解(有可能可以得到,也有可能得不到)。那这个方法是啥呢?就是我们的动态规划算法。
那大家可以自行判断这个题为啥可以用动态规划:①最优子结构 ②子问题重叠
那接下来我们正式进入这个题的讲解,系好安全带,发车喽!!!!!

上图是对这个题的一个初步解释和前提题要,那接下来进入动态规划五步法:
1、确定dp二维数组中元素的含义
这个题的dp二维数组的含义应该很好理解吧,跟矩阵连乘一样的,就是区间i~j合并的最小代价。
2、确定状态转移方程,这个稍后解释
3、确定dp数组的初始化,这个稍后解释
4、确定遍历的顺序,需要几重循环,每个循环分别代表什么意思
大家觉得要几重循环,很明显3重对吧,第一重是区间的长度,从2~n对吧。
第二重是区间的起点,也就是i的值(我写的矩阵连乘和石子合并,用了同样的变量名,是为了方便大家理解,是一个意思)。
第三重就是k的值,也就是你要在哪个位置将其一分为二。
5、更新(遍历)dp数组,将值填入dp数组。这个不解释了啊,这么多动态规划的题讲下来,这个步骤是干啥的你要在不知道,多少有点伤可爱的心了。
那我们开始讲解第2步和第3步,先上代码:
for(int len=2;len<=a.size();len++)
{
for(int i=1;i+len-1<=a.size();i++)
{
int j=i+len-1;
for(int k=i;k<j;k++)
{
//真的只有这个状态转移方程不一样
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
}
}
}然后我们用图给出解释:
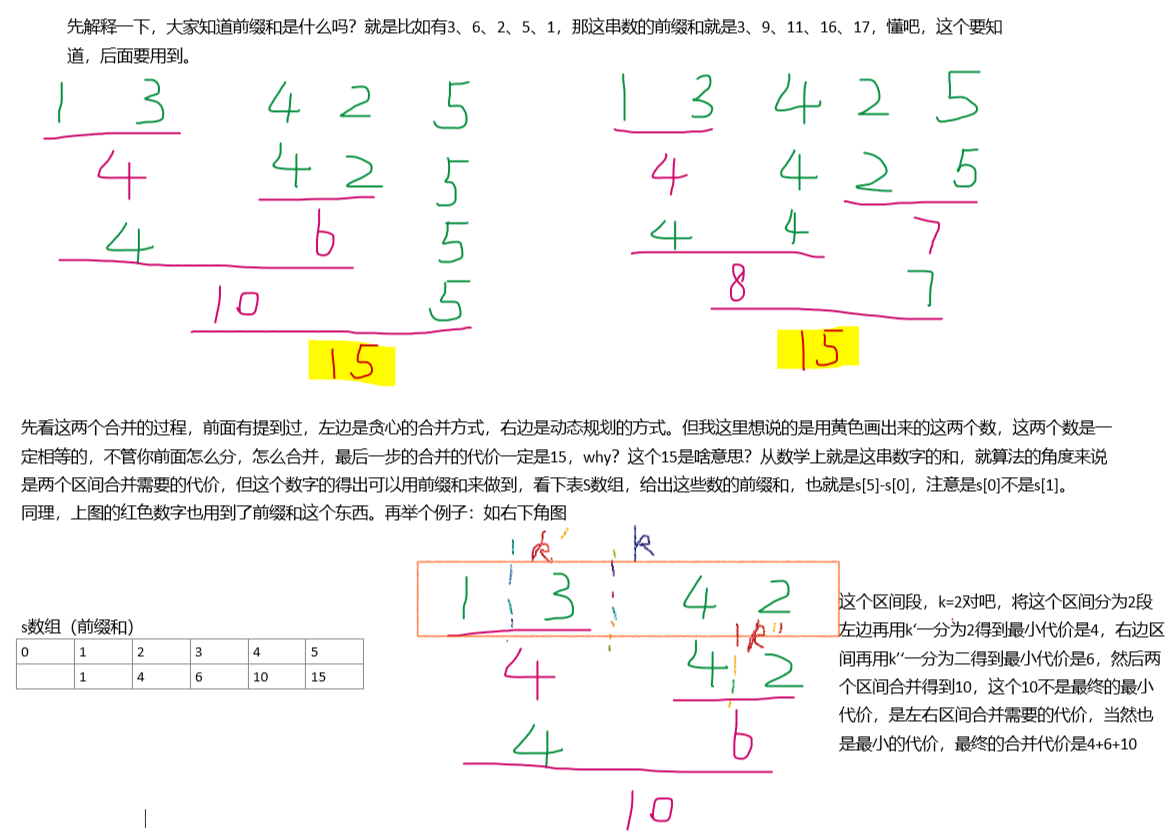
那现在再看下那个状态转移方程,是否有点懂了呢?
接下来我将带大家结合dp二维数组来看看这个状态方程在代码中是怎么起作用的:
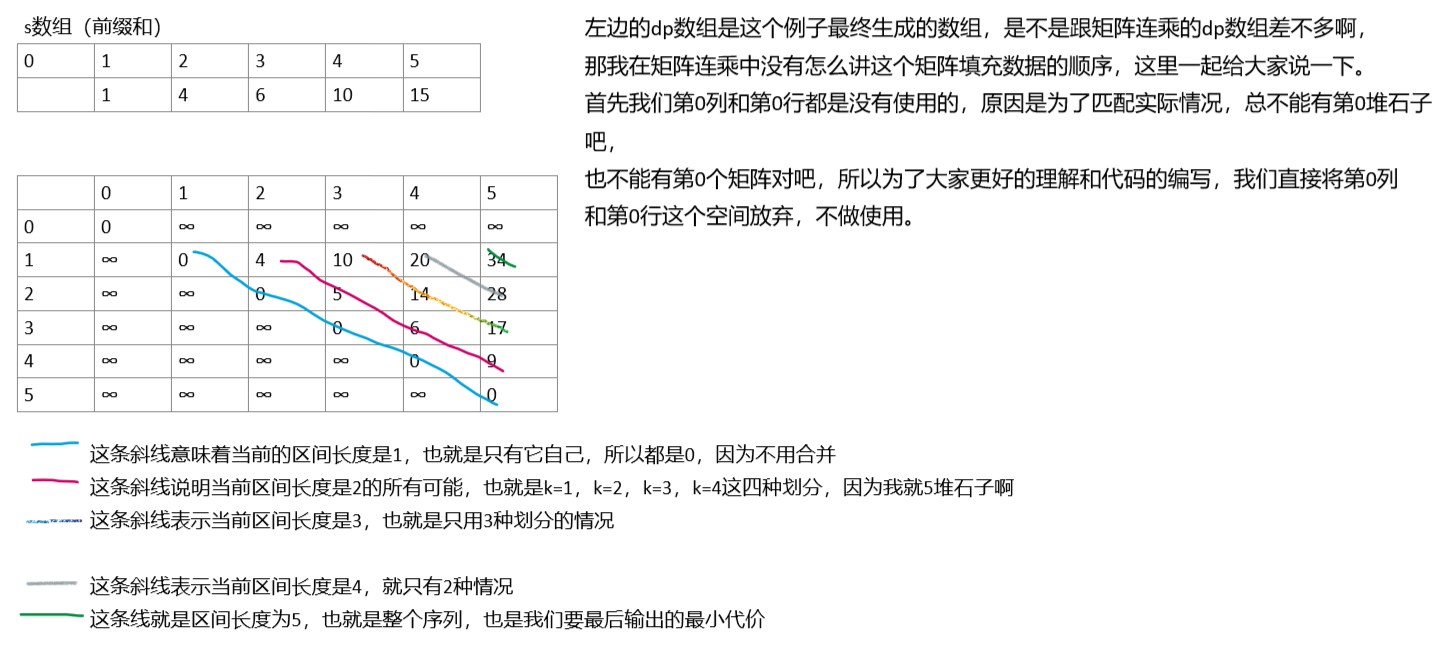
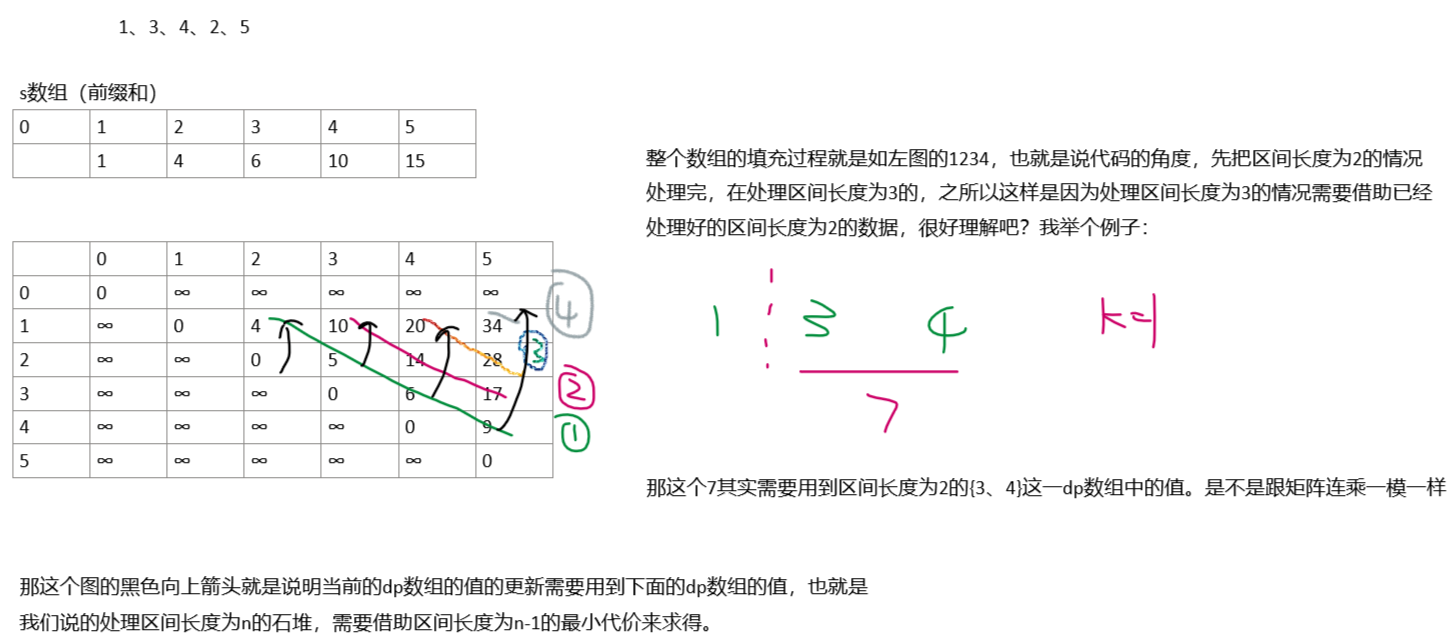
到这里基本上就解释完毕了,大家看完这个解释可以回头去看看矩阵连乘,看当初不理解的地方,现在是否懂了。
那最后dp数组初始化的问题是不是知道答案了,很明显除了对角线全给0,其余均初始化为正无穷,因为我们要去最小值么。
那最后给出执行代码供大家理解:
#include<iostream>
#include<vector>
#include<iomanip>
using namespace std;
#define N 5
vector<int> a={0,1,3,2,4,5};
vector<int> s(a.size()+1);
vector<vector<int>> dp(a.size()+1,vector<int>(a.size()+1,INT32_MAX));
void func()
{
for(int len=2;len<=a.size();len++)
{
for(int i=1;i+len-1<=a.size();i++)
{
int j=i+len-1;
for(int k=i;k<j;k++)
{
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
}
}
}
cout<<dp[1][N-1]<<endl;
}
int main()
{
for(int i=1;i<a.size();i++)
{
s[i]=s[i-1]+a[i];
dp[i][i]=0;
}
func();
for(int i=0;i<a.size();i++)
{
for(int j=0;j<a.size();j++)
cout<<setw(10)<<dp[i][j]<<" ";
cout<<endl;
}
return 0;
}



Comments | NOTHING