最大子序列的和——暴力求解
本篇开始我将给大家介绍最大子序列和,我给大家写了3种解法,分别是暴力求解、贪心、动态规划。
先来看一下暴力求解,这个比较好理解,就是双循环,每个子序列全部遍历一遍,用_count记录当前子序列的和,result记录最大子序列的和,
long long int result=INT64_MIN,就不能给int类型,这里注意#include<iostream>
#include<vector>
using namespace std;
vector<int> arr={-2,1,10,20,-21,5,9};
int _count=0;
int result=INT32_MIN;
void func()
{
for(int i=0;i<arr.size();i++)
{
//刷新实时的最大值,
_count=0;
for(int j=i;j<arr.size();j++)
{
_count+=arr[j];
result = _count > result ? _count:result;
}
}
cout<<result<<endl;
}
int main()
{
func();
return 0;
}最大子序列的和——贪心
看完上面得暴力求解后,是不是发现这个算法不太高效,有点慢,时间复杂度O(n²),那我们这里换一个算法——贪心。
看到贪心,我们就要先研究3个问题:
- 本题中贪心它贪了啥
- 局部最优是啥
- 全局最优是啥
贪心:如果当前有一个序列{-2,1},那么一定是从1开始计算子序列和,因为负数只会拉低总和,这就是贪的地方。
局部最优:当我们的局部子序列和是负数,那么直接舍弃,从下一个元素重新开始计算子序列和,比如{-2,1,10,-21,3,4},当我们发现{-2,1,10,-21}这个子序列的和是负数,那么直接丢弃,从3开始计算子序列和,大家可以自己试试,看是不是这样。
那完整代码如下所示,大家可以自己试试:
#include<iostream>
#include<vector>
using namespace std;
vector<int> arr={-2,1,10,20,-21,5,9};
int _count=0;
int result=INT32_MIN;
void func()
{
for(int i=0;i<arr.size();i++)
{
_count+=arr[i];
if(_count>result) //和暴力求解一样的,用_count不断更新最大值赋给result
result=_count;
if(_count<=0) //当_count为负数时,直接舍弃前面的所有数。
_count=0;
}
cout<<result<<endl;
}
int main()
{
func();
return 0;
}最大子序列的和——动态规划
那贪心介绍完了,我们再来介绍一下用动态规划实现这个算法,依旧是五步走:
1、确定dp数组的含义及下标的含义:dp[i]是包括下标i之前的最大连续子序列和
2、确定递推公式,这个稍后做解释
3、dp数组的初始化,主要是初始化dp[0],其他元素你给任意值就行
4、确定遍历顺序,需要几重循环,是倒序还是正序
5、遍历(更新)dp数组
这里重点解释第二步:
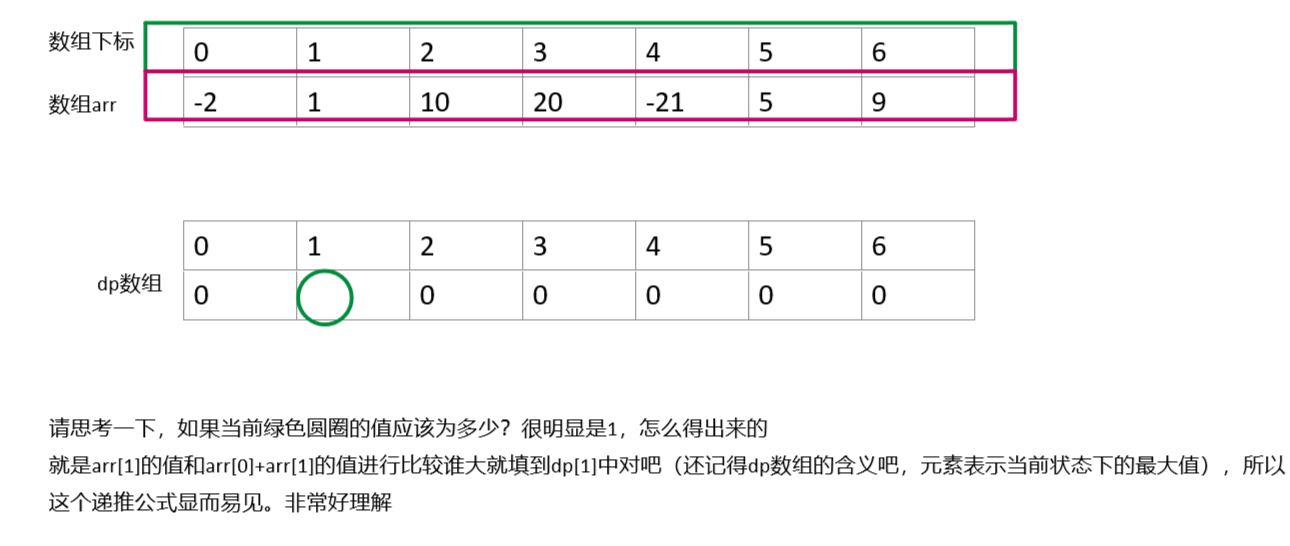
再解释一下第4点:
这里需要像0-1背包问题那样用两个循环嘛?答案是不需要对吧,也不需要倒序遍历,正序即可。
下面是执行代码,大家可以动手运行一下,不懂的可以单步调试一下:
#include<iostream>
#include<vector>
using namespace std;
vector<int> arr={-2,1,10,20,-21,5,9};
vector<int> dp(arr.size());
int result;
void func()
{
dp[0]=arr[0];
result=dp[0];
for(int i=1;i<dp.size();i++)
{
dp[i]=max(dp[i-1]+arr[i],arr[i]);
if(dp[i]>result)
result=dp[i];
}
cout<<result<<endl;
}
int main()
{
func();
return 0;
}这里需要注意一个问题:

最大公共子序列(LCS)
学完了最大子序列和问题,我们来进一步学一下最大公共子序列问题,在学之前我先说明一下什么是最大公共子序列,如下图:

看完上面那张图,我们正式进入LCS问题,安全带系好,可爱要发车了。
大家应该看过课本上对最大公共子序列的描述,可爱在这里呈现一下:

是不是很懵,好官方的语言是吧。咱们不管他,按照可爱的来,学会了后再回去看就懂了。
首先我们给出一个具体的例子,并且做出前提提要,如下图:
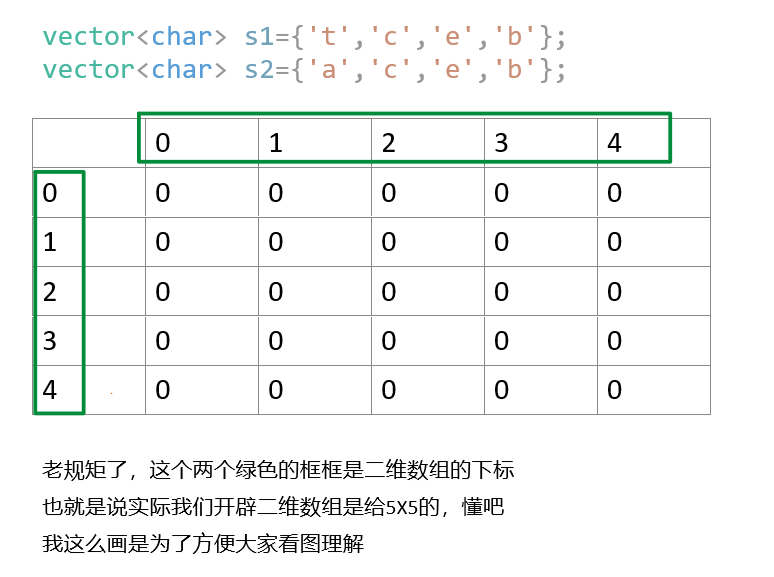
那上图有两个字符数组,直观上看最大公共子序列是啥?很明显{'c','e','b'},且长度为3。我们先说一下这个长度怎么求得,如下图:

看完上图,应该对这个过程有了一个初步的了解,那这个跟动态规划有啥关系呢?其实这里的长度是不是随着遍历的进行会变化,这个变化我们是不是得拿一个东西记录一下,我们就是用dp二维数组记录。
那既然要用动态规划,那就少不了我们的五步走:
- 1、确定dp数组的含义及下标的含义
上面说了,我们需要一个东西来记录这个长度的变化,这个东西就是dp二维数组,dp[i][j]在这个题的意思就是s1[0~i]和s2[0~j]匹配的最大公共自序列,后面我会举具体的例子。
- 2、确定递推公式,这个稍后做解释
- 3、dp数组的初始化
这个题初始化清一色给0就行(不建议给其他数值),因为还没遍历,说明s1和s2两个字符数组的匹配情况我们是不知道的,那0的意思就是默认没有匹配的情况。
- 4、确定遍历顺序
这个题用二重循环应该没有什么争议,毕竟两个指针嘛。外循环和内循环也是可以交换的。但是只可以正序遍历,不可以倒序遍历,这个也好理解吧。
- 5、遍历(更新)dp数组,这个稍后做解释
我们先给出核心代码,然后对上面的点做出解释:
for(int i=1;i<=s1.size();i++) //5X5的矩阵
{
for(int j=1;j<=s2.size();j++)
{
if(s1[i-1]==s2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[s1.size()][s2.size()]<<endl;接下来我对上面的点做如下解释,如下图:


解释完后,给大家看下执行代码,还不懂得,可以单步调式然后画个图:
#include<iostream>
#include<vector>
using namespace std;
vector<char> s1={'t','c','e','b'};
vector<char> s2={'a','c','e','b'};
vector<vector<int>> dp(s1.size()+1,vector<int>(s2.size()+1,0));
void func()
{
for(int i=1;i<=s1.size();i++)
{
for(int j=1;j<=s2.size();j++)
{
if(s1[i-1]==s2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
cout<<dp[s1.size()][s2.size()]<<endl;
}
int main()
{
func();
return 0;
}那这个最大公共子序列的代码对字符数组和数字都有用的,我这里给了字符数组,大家可以写一个整数或者小数试试,是OK的。
那到这里可爱就有个想法,你这用字符数组,整型啥的还得重新修改代码,好慢呢~这个时候C++的模板不就起作用了吗?那我用类模板的方式来实现,大家可以看一看,附加的:
//这里先空着,代码有点语法问题,400码的速度解决ing~~到这里大家可能会有疑问,哎?你这个跟参考书的代码不一样耶,为啥呀?
真的不一样吗?其实是一样的,见下图的解释:

讲完了长度,我们进入正题——输出最大公共子序列的具体内容,那这里dp二维数组就不够了,还需要一个数组b做辅助,这个数组b是干嘛的呢?为啥需要这个b数组啊?
见下图的解释:
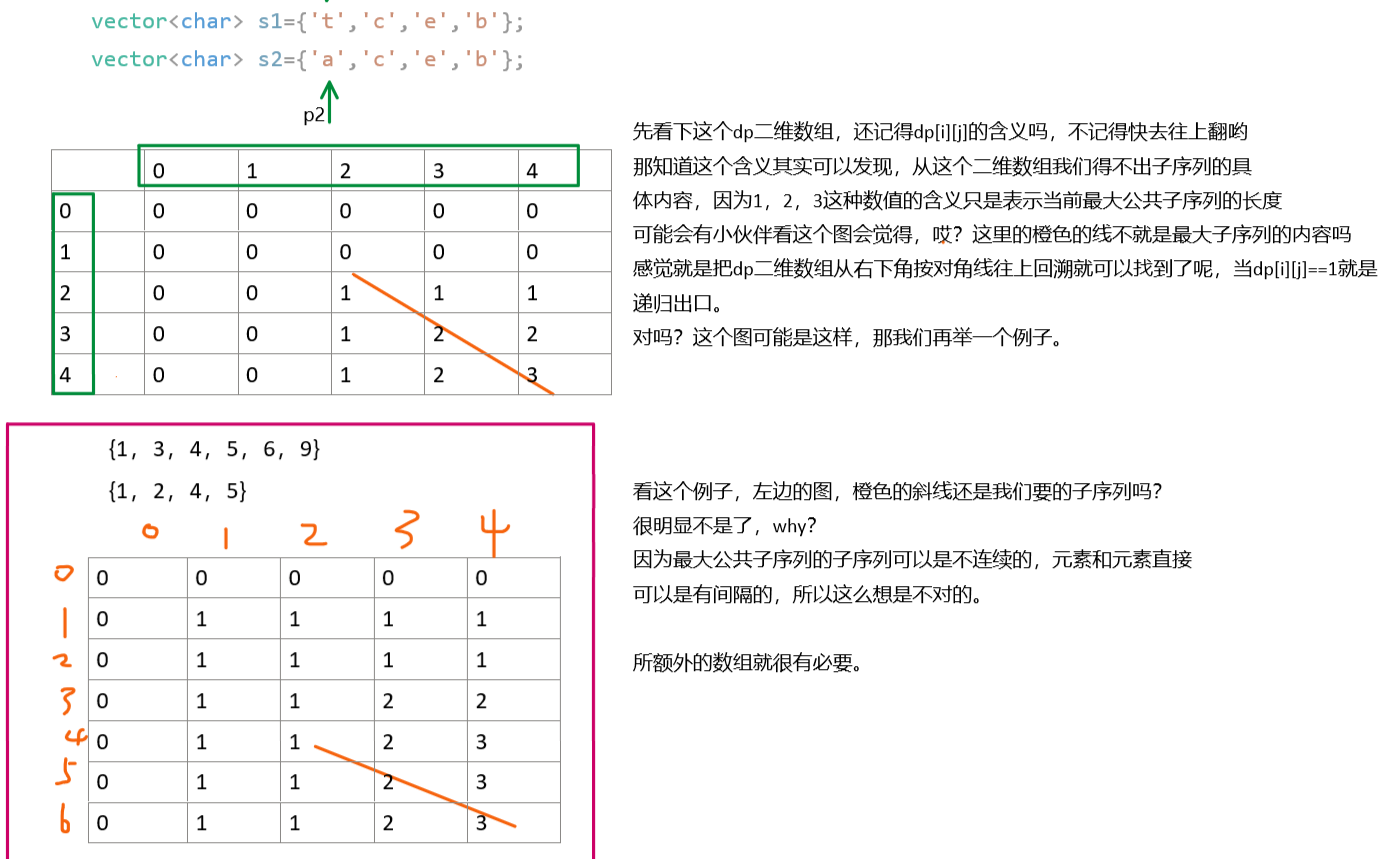
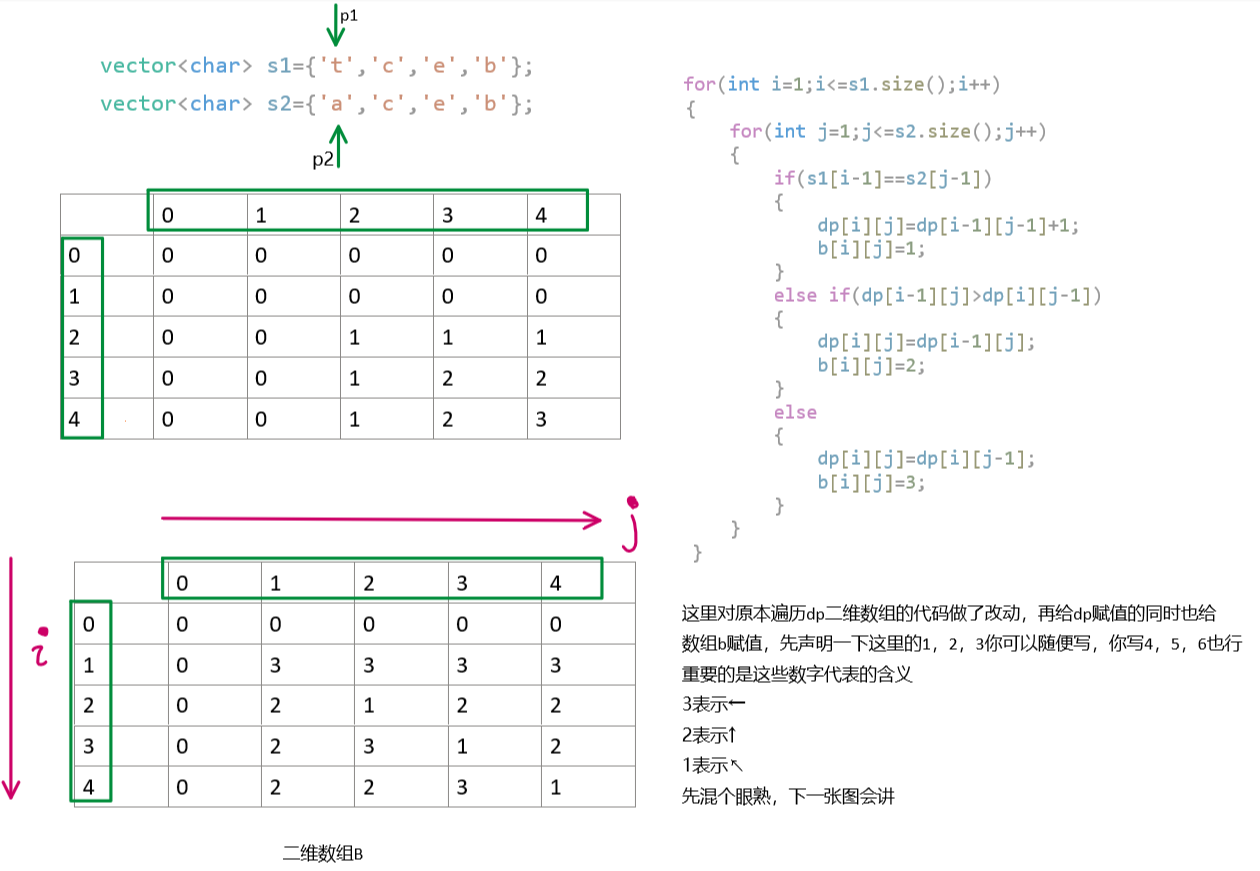

那如果你这个递归绕不过来,可爱再给你画个图:
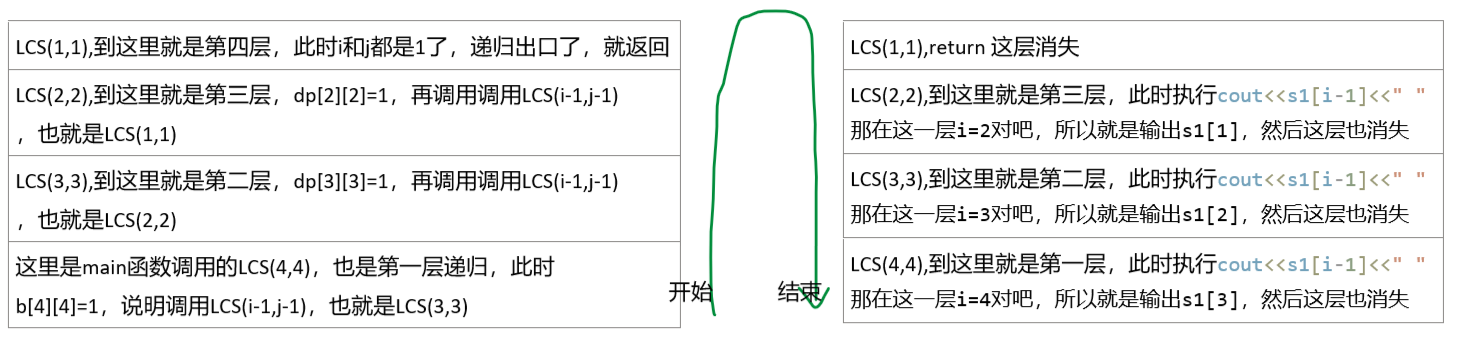
那到这里就讲完了,累死可爱了,最后给出执行代码,大家可以自己运行,也可以改成类模板或者函数模板。
#include<iostream>
#include<vector>
using namespace std;
vector<char> s1={'t','c','e','b'};
vector<char> s2={'a','c','e','b'};
vector<vector<int>> dp(s1.size()+1,vector<int>(s2.size()+1,0));
vector<vector<int>> b(s1.size()+1,vector<int>(s2.size()+1,0));
void LCS(int i,int j)
{
if(i==1||j==1)
return;
if(b[i][j]==1)
{
LCS(i-1,j-1);
cout<<s1[i-1]<<" ";
}
else if(b[i][j]==2)
LCS(i-1,j);
else
LCS(i,j-1);
}
void func()
{
for(int i=1;i<=s1.size();i++)
{
for(int j=1;j<=s2.size();j++)
{
if(s1[i-1]==s2[j-1])
{
dp[i][j]=dp[i-1][j-1]+1;
b[i][j]=1;
}
else if(dp[i-1][j]>dp[i][j-1])
{
dp[i][j]=dp[i-1][j];
b[i][j]=2;
}
else
{
dp[i][j]=dp[i][j-1];
b[i][j]=3;
}
}
}
cout<<dp[s1.size()][s2.size()]<<endl;
}
int main()
{
func();
LCS((int)s1.size(),(int)s2.size());
return 0;
}



Comments | 1 条评论
Your website has quickly become my preferred source for motivation. Thank you for sharing your thoughts.